Explore the limits of modern physics
One of the major goals of theoretical physics is to discover a theoretical framework for unifying gravity with the other three known forces, electromagnetism, and the weak and strong nuclear forces. A unified theory must be compatible with quantum theory at very small scales, which correspond to very high energies. Even the goal of reconciling general relativity with quantum theory has been elusive and will likely require new concepts to accomplish. Quantum effects are expected to play a key role in determining the effective nature of space-time that emerges as general relativity in the classical continuum limit. A wide variety of suggested Planck-scale physics scenarios have explored the idea that Lorentz invariance (LI) may be only valid as an approximation, and have proposed the possibility of Lorentz Invariance Violation (LIV). One result of such assumptions is a modification of the dispersion relation that relates the energy and momentum of a free particle or photon. One of the consequences is that electromagnetic waves of opposite circular polarizations will propagate with different velocities, which leads to a rotation of linear polarization direction proportional to the propagation time and the square of the plane wave number k. Therefore, if polarization is seen in a distant source, it puts constraints on the parameter ξ which controls the rotation angle. Besides, the higher the wave number k, the stronger the rotation effect will be. Thus, the depolarizing effect of space-time induced birefringence will be most pronounced in the gamma-ray energy range.
The best secure bound on this effect, |ξ| < 10-14, was obtained using the observed polarized soft gamma-ray emission from a Gamma-Ray Burst with INTEGRAL (see Figure). On the other hand, the absence of any detection or the observation of a systematic energy dependence of the polarization angle would be a clear sign of the existence of the vacuum birefringence due to Lorentz invariance violation.
Required instrument performances:
The main requirement is on the polarimetry sensitivity, as we need to measure precisely the angle difference between two energy bands. To observe Gamma-Ray Bursts, a large field of view would be, of course, preferable but LIV may be also measured from pointed observations of selected high redshift sources, such as blazars. Gamma-Ray Bursts have to be identified in optical in order to measure as precisely as possible their distance; an angular resolution of around 0.05° is then mandatory to get a more constrained GRB position with robotic telescopes and make a redshift measurement with on-ground bigger telescopes, such as CFHT. Also, as the possible intrinsic change of the polarimetric angle during the GRB duration may result in a null integrated signal, a timing resolution of the order of 1 s is preferable to produce time-resolved polarimetry.
The best secure bound on this effect, |ξ| < 10-14, was obtained using the observed polarized soft gamma-ray emission from a Gamma-Ray Burst with INTEGRAL (see Figure). On the other hand, the absence of any detection or the observation of a systematic energy dependence of the polarization angle would be a clear sign of the existence of the vacuum birefringence due to Lorentz invariance violation.
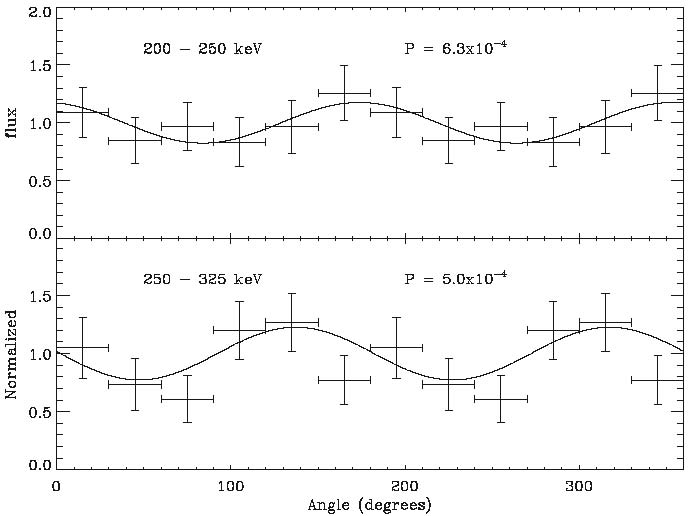
Scatter angle distributions of the gamma-ray emission observed with INTEGRAL/IBIS during 10 s of the gamma-ray burst GRB041219A in two energy bands: 200–250 keV (upper panel) and 250–325 keV (lower panel). These distributions are consistent with a highly polarized signal (the chance probability of a non-polarized signal is reported in each panel), which provides a strong constraint on Lorentz Invariance Violation. Credit: P. Laurent et al. 2011, Phys. Rev. D 83, 121301(R)
|
Required instrument performances:
The main requirement is on the polarimetry sensitivity, as we need to measure precisely the angle difference between two energy bands. To observe Gamma-Ray Bursts, a large field of view would be, of course, preferable but LIV may be also measured from pointed observations of selected high redshift sources, such as blazars. Gamma-Ray Bursts have to be identified in optical in order to measure as precisely as possible their distance; an angular resolution of around 0.05° is then mandatory to get a more constrained GRB position with robotic telescopes and make a redshift measurement with on-ground bigger telescopes, such as CFHT. Also, as the possible intrinsic change of the polarimetric angle during the GRB duration may result in a null integrated signal, a timing resolution of the order of 1 s is preferable to produce time-resolved polarimetry.
| Performance parameter | Goal value | Remarks and notes |
|
Field-of-view (FWHM, deg) |
180° | Smaller FOV is also possible |
|
Angular resolution (FWHM, deg) |
~ 0.05° (GRB) |
To measure GRB position, less necessary for known sources (blazars) |
|
Spectral resolution (ΔE/E @ Energy) |
10% | |
|
Line sensitivity (@ Energy) (cm-2 s-1, 3σ, 1 Ms) |
N/A | |
|
Continuum sensitivity (in which energy band?) (cm-2 s-1 keV-1, ΔE=E, 3σ, 1 Ms) |
|
|
| Timing performances | 1 s | To produce time-resolved polarimetry |
| Polarimetric capability | 5% | Sources seems to be strongly polarized, but a high sensitivity is mandatory to ensure a good polarization angle measurement |
| Real-time data? | no |
 AstroMeV
AstroMeV